Andres Felipe Moncada Montoya
10-03
Instituto Tecnológico
Justificación:
Con este block se les mostrara detalladamente que es caída libre y movimiento parabólico, algunos ejercicios y mucho mas.
Objetivos:
-Encuesta pre-saberes
-Historieta
-Mapa mental
-Teoría general
-Vídeos
-Simulación en java
-Imágenes
-Crucigrama
-Sopa de letras
Encuesta pre-saberes
Responda los numerales 1 y 72 de acuerdo al texto siguiente:
Si un cuerpo se deja caer su velocidad inicial es cero y la altura que ha descendido se puede calcular mediante la expresión:
h = v2/2g.
De esta ecuación se puede asegurar que en la caída libre la altura (h) que ha descendido un cuerpo y la velocidad al cuadrado (v2) que lleva en esa posición, son directamente proporcionales. Dos cuerpos se dejan caer desde alturas, h1 y h2, se observa que al llegar al piso v2 (Velocidad final del cuerpo lanzado desde h2) es el doble de v1 (Velocidad final del cuerpo lanzado desde la altura h1).
1. Puede afirmarse que:
A. h1 = h2
B. h1 = ½ h2
C. h2 = 4h1
D. h1 = 2h2
A. h1 = h2
B. h1 = ½ h2
C. h2 = 4h1
D. h1 = 2h2
1. Es incorrecto afirmar, al comparar las alturas y sus respectivas velocidades en la ecuación general h = v2/2g, que:
A. h1 = v22 /8g
B. h1 = v12 /2g
C. h2 = 2v12 /g
D. h2 = 4v12 /g
A. h1 = v22 /8g
B. h1 = v12 /2g
C. h2 = 2v12 /g
D. h2 = 4v12 /g
3.
La velocidad y la altura también se pueden expresar en función del tiempo t, mediante las ecuaciones:
La velocidad y la altura también se pueden expresar en función del tiempo t, mediante las ecuaciones:
v = vo + gt
h = vot + gt2/2
donde vo es la velocidad inicial.
El tiempo de caída de ambos cuerpos se relacionan según:
A. t2 = t1
B. t2 = ½ t1
C. t2 = 2 t1
D. t2 = 4 t1
B. t2 = ½ t1
C. t2 = 2 t1
D. t2 = 4 t1
4.
En una segunda prueba, se comienza a halar el cuerpo que se encuentra inicialmente en reposo, incrementando lentamente la fuerza hasta que con una fuerza F se pone en movimiento. Con los datos tomados se puede estimar:
En una segunda prueba, se comienza a halar el cuerpo que se encuentra inicialmente en reposo, incrementando lentamente la fuerza hasta que con una fuerza F se pone en movimiento. Con los datos tomados se puede estimar:
A. La aceleración que toma el cuerpo.
B. La velocidad que adquiere el cuerpo.
C. El coeficiente de fricción estático de la superficie.
D. El coeficiente de fricción cinético de la superficie.
B. La velocidad que adquiere el cuerpo.
C. El coeficiente de fricción estático de la superficie.
D. El coeficiente de fricción cinético de la superficie.
5.
Un vehículo se encuentra detenido y averiado sobre una carretera plana. Dos hombres comienzan a empujarlo, a los dos segundos la velocidad es de 1 m/s, a los 4 segundos es de 2 m/s
Un vehículo se encuentra detenido y averiado sobre una carretera plana. Dos hombres comienzan a empujarlo, a los dos segundos la velocidad es de 1 m/s, a los 4 segundos es de 2 m/s
Se puede concluir que:
A. Los hombres realizan durante los primeros 4 segundos la misma fuerza.
B. Los hombres realizan durante los primeros 4 segundos una fuerza cada vez mayor.
C. Los hombres realizan durante los primeros 4 segundos una fuerza cada vez menor.
D. Los hombres realizan durante los primeros 2 segundos una fuerza y luego hasta los 4 segundos una fuerza del doble de la anterior.
B. Los hombres realizan durante los primeros 4 segundos una fuerza cada vez mayor.
C. Los hombres realizan durante los primeros 4 segundos una fuerza cada vez menor.
D. Los hombres realizan durante los primeros 2 segundos una fuerza y luego hasta los 4 segundos una fuerza del doble de la anterior.
6. La aceleración gravitacional en la Luna es cerca de 1/6 de la aceleración en la Tierra. Si sobre la superficie de la Luna usted pudiera lanzar un balón hacia arriba con la misma velocidad que sobre la superficie de la Tierra, ¿Cuál de las siguientes afirmaciones sería correcta?
A. a. El balón tarda el mismo tiempo en alcanzar la máxima altura en la Luna que en la Tierra.
B. El balón tardaría seis veces más del tiempo en la Luna que el tiempo que tarda en la Tierra.
C. El balón tardaría seis veces más del tiempo en la Tierra que el tiempo que tarda en la Luna.
D. El balón tardaría 1/6 del tiempo en la Luna que el tiempo que tarda en la Tierra.
B. El balón tardaría seis veces más del tiempo en la Luna que el tiempo que tarda en la Tierra.
C. El balón tardaría seis veces más del tiempo en la Tierra que el tiempo que tarda en la Luna.
D. El balón tardaría 1/6 del tiempo en la Luna que el tiempo que tarda en la Tierra.
7. Un pesista levanta una masa m, ¿Cómo es la fuerza F que ejerce el pesista comparada con el peso que levanta?
A. F > mg
B. mg > F
C. F ≥ mg
D. F = mg
A. F > mg
B. mg > F
C. F ≥ mg
D. F = mg
8. El mismo pesista levanta ahora la masa m desde la cintura hasta la altura de sus brazos extendidos, en total 120 cm, para lo cual realiza un impulso inicial de una vez y media la gravedad. Se puede afirmar que la fuerza F que debió realizar inicialmente para levantar la masa m se puede expresar mediante:
A. F > mg
B. F=mg
C. F ≥ mg
D. F < mg
B. F=mg
C. F ≥ mg
D. F < mg
Resuelva las preguntas 4 y 5 con base en la siguiente información:
La presión es la relación entre la fuerza ejercida y el área sobre la cual se aplica dicha fuerza.
P = F / A
En un líquido la presión P es proporcional a la profundidad H (P = dgH, donde d es la densidad del líquido y g es la gravedad). Si usted tiene dos cajas de vidrio, la primera es un cubo perfecto con arista de lado a y la otra caja tiene base cuadrada del mismo lado a que la primera y de altura 2a, si las dos cajas se sellan herméticamente y se sumergen hasta el fondo de una piscina,
9. Podemos afirmar que:
A. La presión total sobre la primera caja es mayor que la presión sobre la segunda caja, ya que si bien la base se encuentra a la misma profundidad que la segunda caja, su cara superior está más profunda.
B. La presión total sobre la primera caja es menor que la presión sobre la segunda caja, ya que la segunda caja tiene más área.
C. La presión total sobre la primera caja es igual que la presión sobre la segunda caja ya que ambas cajas se encuentran a la misma profundidad.
A. La presión total sobre la primera caja es mayor que la presión sobre la segunda caja, ya que si bien la base se encuentra a la misma profundidad que la segunda caja, su cara superior está más profunda.
B. La presión total sobre la primera caja es menor que la presión sobre la segunda caja, ya que la segunda caja tiene más área.
C. La presión total sobre la primera caja es igual que la presión sobre la segunda caja ya que ambas cajas se encuentran a la misma profundidad.
D. La presión total sobre la primera caja es la mitad que la presión sobre la segunda caja, por tener la mitad de su altura.
10. Si ambas cajas están hechas del mismo tipo de material, al llevarlas a una profundidad a la cual se lleva al límite la resistencia de este material, es más factible
A. que se rompa inicialmente la primera caja.
B. que se rompa primero la segunda caja.
C. que se rompa la primera o la segunda caja es cuestión del azar, es decir, resulta impredecible.
D. que se rompan simultáneamente las cajas.
Historieta:
B. que se rompa primero la segunda caja.
C. que se rompa la primera o la segunda caja es cuestión del azar, es decir, resulta impredecible.
D. que se rompan simultáneamente las cajas.
Historieta:
Mapa conceptual:
Teoria:
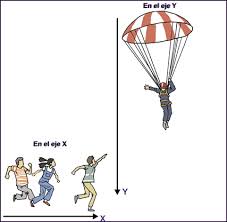
Movimiento parabólico
En realidad, cuando se habla de cuerpos que se mueven en un campo gravitatorio central (como el de La Tierra), el movimiento es elíptico. En la superficie de la Tierra, ese movimiento es tan parecido a una parábola que perfectamente podemos calcular su trayectoria usando la ecuación matemática de una parábola. La ecuación de una elipse es bastante más compleja. Al lanzar una piedra al aire, la piedra intenta realizar una elipse en uno de cuyos focos está el centro de la Tierra. Al realizar esta elipse inmediatamente choca con el suelo y la piedra se para, pero su trayectoria es en realidad un "trozo" de elipse. Es cierto que ese "trozo" de elipse es casi idéntico a un "trozo" de parábola. Por ello utilizamos la ecuación de una parábola y lo llamamos "tiro parabólico". Si nos alejamos de la superficie de la Tierra sí tendríamos que utilizar una elipse(como en el caso de los satélites artificiales).
El movimiento parabólico puede ser analizado como la composición de dos movimientos rectilíneos: un movimiento rectilíneo uniforme horizontal y un movimiento rectilíneo uniformemente acelerado vertical.
El tiro parabólico tiene las siguientes características:
- Conociendo la velocidad de salida (inicial), el ángulo de inclinación inicial y la diferencia de alturas (entre salida y llegada) se conocerá toda la trayectoria.
- Los ángulos de salida y llegada son iguales.
- La mayor distancia cubierta o alcance se logra con ángulos de salida de 45º.
- Para lograr la mayor distancia fijado el ángulo el factor más importante es la velocidad.
- Se puede analizar el movimiento en vertical independientemente del horizontal.
Tipos de movimiento parabólico[editar]
Movimiento parabólico (completo)[editar]
El movimiento parabólico completo se puede considerar como la composición de un avance horizontal rectilíneo uniforme y un lanzamiento vertical hacia arriba, que es un movimiento rectilíneo uniformemente acelerado hacia abajo (MRUA) por la acción de lagravedad.
En condiciones ideales de resistencia al avance nulo y campo gravitatorio uniforme, lo anterior implica que:
- Un cuerpo que se deja caer libremente y otro que es lanzado horizontalmente desde la misma altura tardan lo mismo en llegar al suelo.
- La independencia de la masa en la caída libre y el lanzamiento vertical es igual de válida en los movimientos parabólicos.
- Un cuerpo lanzado verticalmente hacia arriba y otro parabólicamente completo que alcance la misma altura tarda lo mismo en caer.
- El tiempo que tarda en alcanzar su altura máxima es el mismo tiempo que tarda en recorrer la mitad de su distancia horizontal, es decir, el tiempo total necesario para alcanzar la altura máxima y regresar al suelo es el mismo para el total de recorrido horizontal.
Ecuaciones del movimiento parabólico[editar]
Hay dos ecuaciones que rigen el movimiento parabólico:
donde:
 es el módulo de la velocidad inicial.
es el módulo de la velocidad inicial. es el ángulo de la velocidad inicial sobre la horizontal.
es el ángulo de la velocidad inicial sobre la horizontal. es la aceleración de la gravedad.
es la aceleración de la gravedad. son dos versores (vectores unitarios) en el plano.
son dos versores (vectores unitarios) en el plano.
La velocidad inicial se compone de dos partes:
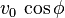 que se denomina componente horizontal de la velocidad inicial.
que se denomina componente horizontal de la velocidad inicial.
- En lo sucesivo

- En lo sucesivo
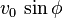 que se denomina componente vertical de la velocidad inicial.
que se denomina componente vertical de la velocidad inicial.
- En lo sucesivo
- En lo sucesivo
Se puede expresar la velocidad inicial de este modo:
 : [ecu. 1]
: [ecu. 1]
Será la que se utilice, excepto en los casos en los que deba tenerse en cuenta el ángulo de la velocidad inicial.
Ecuación de la aceleración[editar]
La única aceleración que interviene en este movimiento es la constante de la gravedad, que corresponde a la ecuación:
que es vertical y hacia abajo.
Ecuación de la velocidad[editar]
La velocidad de un cuerpo que sigue una trayectoria parabólica se puede obtener integrando la siguiente ecuación:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
Ecuación de la posición[editar]
Partiendo de la ecuación que establece la velocidad del móvil con la relación al tiempo y de la definición de velocidad, la posición puede ser encontrada integrando de la siguiente ecuación diferencial:
La integración es muy sencilla por tratarse de una ecuación diferencial de primer orden y el resultado final es:
Caída libre
En física, se denomina caída libre al movimiento de un cuerpo bajo la acción exclusiva de un campo gravitatorio. Esta definición formal excluye a todas las caídas reales influenciadas en mayor o menor medida por la resistencia aerodinámica del aire, así como a cualquier otra que tenga lugar en el seno de un fluido; sin embargo, es frecuente también referirse coloquialmente a éstas como caídas libres, aunque los efectos de la viscosidaddel medio no sean por lo general despreciables.
El concepto es aplicable también a objetos en movimiento vertical ascendente sometidos a la acción desaceleradora de la gravedad, como undisparo vertical; o a cualquier objeto (satélites naturales o artificiales, planetas, etc.) en órbita alrededor de un cuerpo celeste. Otros sucesos referidos también como caída libre lo constituyen las trayectorias geodésicas en el espacio-tiempo descritas en la teoría de la relatividad general.
Ejemplos de caída libre deportiva los encontramos en actividades basadas en dejarse caer una persona a través de la atmósfera sin sustentaciónalar ni de paracaídas durante un cierto trayecto.1 2
La caída libre como sistema de referencia[editar]
Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que se esté usando.
En la física clásica, la fuerza gravitatoria que se ejerce sobre una masa es proporcional a la intensidad del campo gravitatorio en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece elprincipio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica. Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para cada marco teórico son completamente diferentes.
Caída libre ideal[editar]
Véase también: Ecuaciones para un cuerpo en caída libre
En la caída libre ideal, se desprecia la resistencia aerodinámica que presenta el aire al movimiento del cuerpo, analizando lo que pasaría en elvacío. En esas condiciones, la aceleración que adquiriría el cuerpo sería debida exclusivamente a la gravedad, siendo independiente de su masa; por ejemplo, si dejáramos caer una bala de cañón y una pluma en el vacío, ambos adquirirían la misma aceleración,  , que es la aceleración de la gravedad
, que es la aceleración de la gravedad
 , que es la aceleración de la gravedad
, que es la aceleración de la gravedadEcuación del movimiento[editar]
De acuerdo a la segunda ley de Newton, la fuerza  que actúa sobre un cuerpo es igual al producto de su masa
que actúa sobre un cuerpo es igual al producto de su masa  por la aceleración que adquiere. En caída libre sólo intervienen el peso
por la aceleración que adquiere. En caída libre sólo intervienen el peso  (vertical, hacia abajo) y el rozamiento aerodinámico
(vertical, hacia abajo) y el rozamiento aerodinámico 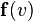 en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
 que actúa sobre un cuerpo es igual al producto de su masa
que actúa sobre un cuerpo es igual al producto de su masa  por la aceleración que adquiere. En caída libre sólo intervienen el peso
por la aceleración que adquiere. En caída libre sólo intervienen el peso  (vertical, hacia abajo) y el rozamiento aerodinámico
(vertical, hacia abajo) y el rozamiento aerodinámico 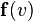 en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
en la misma dirección, y sentido opuesto a la velocidad. Dentro de un campo gravitatorio aproximadamente constante, la ecuación del movimiento de caída libre es:
La aceleración de la gravedad  lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.
lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.
 lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.
lleva signo negativo porque se toma el eje vertical como positivo hacia arriba.Trayectoria en caída libre[editar]
Caída libre totalmente vertical[editar]
El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleracióng) (aproximadamente porque la velocidad aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:
(1)
donde:
 , son la aceleración y la velocidad verticales.
, son la aceleración y la velocidad verticales. , es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).
, es la fuerza de rozamiento fluidodinámico (que aumenta con la velocidad).
- Si, en primera aproximación, se desprecia la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan velocidades moderadas, la solución de la ecuación diferencial () para las velocidades y la altura vienen dada por:
donde v0 es la velocidad inicial, para una caída desde el reposo v0 = 0 y h0 es la altura inicial de caída.
- Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la resistencia fluidodinámica que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico kw:
(2)
En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial ():
Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:
- Un análisis más cuidadoso de la fricción de un fluido revelaría que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sino turbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad:
(3)
Donde:
 , es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo.
, es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo. , es el área transversal a la dirección del movimiento.
, es el área transversal a la dirección del movimiento.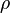 , es la densidad del fluido.
, es la densidad del fluido. , es el signo de la velocidad.
, es el signo de la velocidad.
La velocidad límite puede calcularse fácilmente poniendo igual a cero la aceleración en la ecuación ():
La solución analítica de la ecuación diferencial () depende del signo relativo de la fuerza de rozamiento y el peso por lo que la solución analítica es diferente para un cuerpo que sube o para uno que cae. La solución de velocidades para ambos casos es:
Donde:  .
.
 .
.
Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura  y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial
y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial 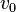 se obtienen los siguientes resultados para la altura del cuerpo:
se obtienen los siguientes resultados para la altura del cuerpo:
 y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial
y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial 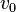 se obtienen los siguientes resultados para la altura del cuerpo:
se obtienen los siguientes resultados para la altura del cuerpo:
Caída libre ( y
y  ):
):
 y
y  ):
):
El tiempo transcurrido en la caída desde la altura  hasta la altura
hasta la altura 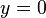 puede obtenerse al reordenar la ecuación anterior:
puede obtenerse al reordenar la ecuación anterior:
 hasta la altura
hasta la altura 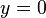 puede obtenerse al reordenar la ecuación anterior:
puede obtenerse al reordenar la ecuación anterior:
Lanzamiento vertical ( y
y 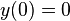 ):
):
 y
y 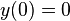 ):
):
Si la altura  es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura  puede calcularse como:
puede calcularse como:
 es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura
es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura  puede calcularse como:
puede calcularse como:
Se puede demostrar que el tiempo que tarda un cuerpo en caer desde una altura  hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de
hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de  si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
 hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de
hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la altura máxima de  si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
sabiendo que  y que
y que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](https://upload.wikimedia.org/math/2/a/8/2a8f254b20cdbb409d09efc8c1990a48.png)
 y que
y que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](https://upload.wikimedia.org/math/2/a/8/2a8f254b20cdbb409d09efc8c1990a48.png)
Intuitivamente la diferencia de tiempos es clara, en el tiro hacia arriba la velocidad inicial es mayor por lo que la fuerza de rozamiento promedio a lo largo de la trayectoria también es mayor que la que se alcanza en tiro hacia abajo.
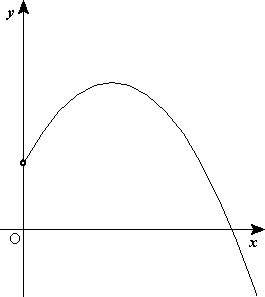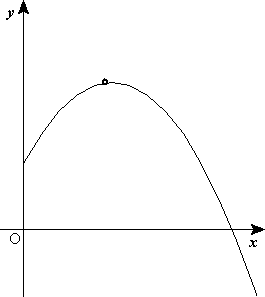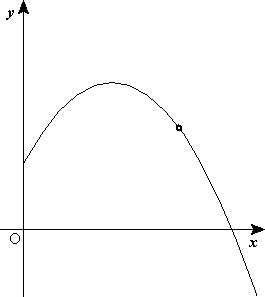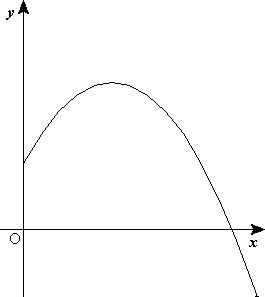
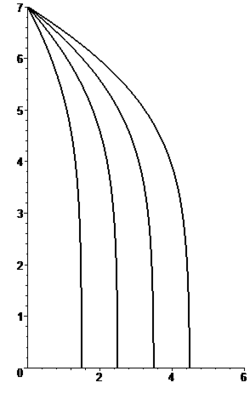
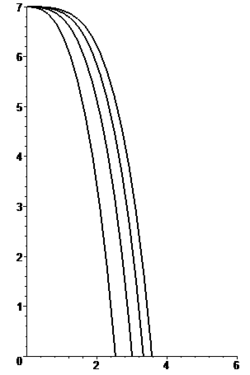
Caída libre parabólica y casi-parabólica[editar]
Cuando un cuerpo cae en caída libre pero no parte del reposo porque tiene una velocidad no nula, entonces la trayectoria de caída no es una recta sino una curva aproximadamente parabólica. La ecuación de la trayectoria en coordenadas cartesianas viene dada por:
(4)
donde x es la coordenada horizontal (eje de abcisas) e y la coordenada vertical (eje de ordenadas).
La expresión de la velocidad vertical debe reescribirse en función de la coordenada x teniendo en cuenta que t = x/vx. Pueden distinguirse los siguientes casos:
- Para un cuerpo en caída libre sin rozamiento, la trayectoria es exactamente una parábola dada por:
- Cuando se incluye el rozamiento aerodinámico, la trayectoria no es exactamente una parábola. Por ejemplo para una fuerza de rozamiento proporcional a la velocidad como en la () la trayectoria resulta ser:
donde:
Para una fuerza de rozamiento proporcional al cuadrado de la velocidad, la integración de las ecuaciones del movimiento es más compleja, presuponiendo fuerzas de rozamiento independientes en dirección horizontal y vertical proporcionales al cuadrado del valor de la componente:
La trayectoria viene dada por:
donde:
Las figuras adjuntas muestran la forma de las trayectorias para cinco valores diferentes del parámetro β para una misma altura de caída (medida en unidades de longitud δ).
VIDEOS
-caida libre
-MOVIMIENTO PARABOLICO
-SIMULACION EN JAVA
-CAIDA LIBRE

-MOVIMIENTO PARABOLICO
-SOPA DE LETRAS
Caída Libre
-CRUSIGRAMA
Conceptos-Caída libre
-






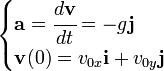

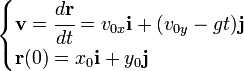












![y(t)=h_0-\cfrac{1}{{\alpha}}\ln\left[\cosh\left(-t\sqrt{{\alpha}{g}}\right) \right]](https://upload.wikimedia.org/math/6/4/4/64407f2d5c666902f084e7350c123773.png)

![y(t)=\cfrac{1}{{\alpha}}\ln\left[\cfrac{\cos\left[-t\sqrt{{\alpha}{g}}+\arctan\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]}{\cos\left[\mbox{arctan}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]} \right]](https://upload.wikimedia.org/math/1/6/2/162a803c65007695a5634885c3c8cce0.png)





![y(x) = h_0 - \delta \left[\frac{x}{\beta\delta}-\ln \left(1-\frac{x}{\beta\delta} \right) \right]](https://upload.wikimedia.org/math/e/3/1/e31cbaa9061dfc54b45dc4e2a0bd7da8.png)



![y(x) = h_0 - \delta \ln \left[\cosh \left( \frac{e^{x/\delta}-1}{\beta}\right) \right]](https://upload.wikimedia.org/math/5/8/0/580d709c14a395cdf8e2edb1ef710981.png)






No hay comentarios:
Publicar un comentario